Pal Analysis
Probing passives probabilities in Palworld. Exploring game mechanisms with empirical data analysis.
Pal Analysis
Note: I initially intended for this analysis to live and die as a post on reddit… adjust your expectations accordingly.
Analysis of 10,000 Captures - A Deep dive on Passive Skill probabilities (Dataset included)
What on earth are you on about?
Palworld is an open-world survival crafting game often caricatured as “Pokémon but with guns”.
Core to the gameplay and indeed its namesake are pals. Pals are the creatures that wander about in the world that you as the player can catch.
Captured pals will join your team and assist with all aspects of the game from combat to base-building, resource gathering, and more. Pals typically specialize in one of these areas of gameplay based on the capabilities unique to each pal (work suitability).
Passive skills are (most often) randomly assigned modifiers that augment certain attributes of a pal. For instance, some change a pal’s damage, some increase movement speed, and some enhance work speed - the rate at which a pal can complete a suitable task.
In the mid-late game, passive skills become a player’s primary focus. The buffs they provide to a pal’s base stats are integral to the player reaching the end-game content.
By the point a player cares about optimizing passive skills, they typically have already encountered all the most desirable passive skills (Rainbow-tier) at least once. Hereafter, a player’s dependence on wild pals is reduced substantially due to the game’s breeding mechanism, which allows passive skills to transfer between pals of different species via inheritance.
Compared to wild capture, breeding is far more efficient at producing desired pal-passive combinations under normal circumstances, earning it the favor of community efforts thus far. Information regarding passive skill assignment in wild pals is far scarcer, limited primarily to anecdotal estimates shared among players.
With this analysis, I hope to help close the knowledge gap between the two means of passive skill acquisition.
Overview
While the mechanisms and probabilities behind breeding passives and IVs have been fairly well documented and explored, the same cannot be said for wild-caught pals. To the best of my knowledge, this is the first formal analysis of wild-caught pal passive skill mechanisms.
The goal is to answer the following questions:
- What is the probability of a wild-caught pal having 0, 1, 2, 3, or 4 passive skills?
- Are all Rainbow passives equally likely?
- Are weak Common passives more likely than strong ones?
- What is the probability of getting a specific Common passive?
- What is the probability of getting a specific/any Rainbow passive?
Bonus Topics
- Two (potentially) novel discoveries about Yakumo’s partner ability that are Complete Game Changers That Will Totally Change How You Use Yakumo!™
-
Clickbait aside, it does contradict the wisdom/advice often shared in the community.
-
- A brief look into random breeding mutations.
TL;DR
(for the CoolTimeReduction_Up_2)
-
(assuming 0 innate)
n-skills p(n-skills) 0 10.5% 1 76% 2 9.6% 3 3% 4 0.9% -
Probably, it might depend on how you treat Lucky
-
yes, in practice
-
~1/60 (1.67%)
-
~1/1110 | ~1/140
Dataset
- All Datasets - Google Sheets
- External data
Data Collection
(this was all done prior to the pal box expansion, and yeah… oof)
For capture data,
- Change world settings to max spawn rate and longest days.
- Create a viewing cage and empty out palbox completely
- Store a backup of the world in this clean state
- Repeat 10x
- Using Homing Sphere Launcher + Sniper Module II, capture Gobfin from Gobfin’s Turf until palbox + 1 viewing cage is entirely filled, yielding a 1000-pal sample.
- Export
Level.savdata tojsonvia palworld-save-tools (note: I have since discovered a maintained fork that works far better) - Reset world by restoring from clean state backup
For Yakumo data,
- Follow the exact same procedure but instead of using a fast flying mount, keep a max-condensed Yakumo with 4 Rainbow passives out the entire duration.
- Perform this only once because, in stark contrast to Yakumo, life moves quickly.
For breeding data,
- Create breeding farms and populate with pairs of blank (0-passive) gobfin.
- Allow to run in background, ever so often gathering all the eggs and storing in chests.
- Again use
palworld-save-toolsto export data, this time observingDynamicItemSaveDatato view passives on stored eggs. - (optional) Realize that using the save-export-restore method would have been a far better approach that could have saved you a ton of time in hindsight while writing your data collection procedure.
Analysis
A note on terminology: I use “passive skills”, “passives”, “skills”, and “traits” interchangeably.
Which one I use depends solely on how I’m feeling at the time. Partner skills will be called by name or as “partner abilities” to make the distinction clear. Active skills will not be discussed at any point.
- “Rainbow” = Rainbow-tier passive skills (Demon God, Swift, etc.) excluding Lucky
- “Common” = everything not Rainbow or Lucky
Number of Passive Skills (Q1)
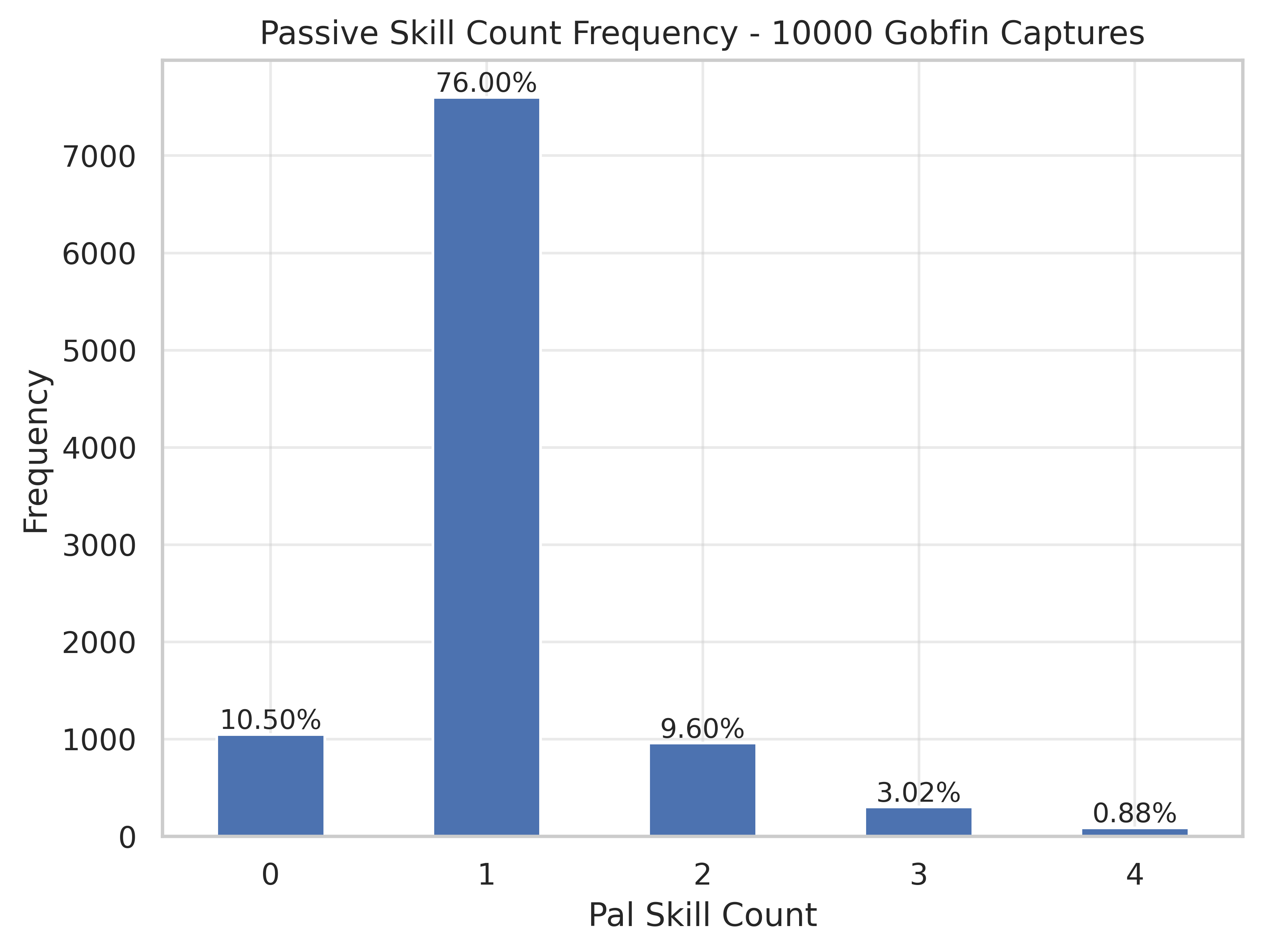
This chart shows a basic count of the number of passive skills on each of the 10,000 captured pals. Given results this extreme, it is fairly safe to assume the probability of a pal having 0-4 skills is not uniform. On average, roughly 3 out of every 4 pals captured have 1 passive skill. This is good news for those who hate breeding off undesirable skills, but also means a higher number of required captures before encountering a particular skill.
Additionally, when hunting for a blank pal for breeding, you can expect it to take ~19 captures for a 0-passive pal of a particular gender (assuming an equal gender ratio).
Considering much of the analysis builds off this data, I feel it’s worthwhile to list the confidence interval for these findings.
| n | p(n) | confidence interval (95%) |
|---|---|---|
| 0 | 10.5% | (9.91; 11.12)% |
| 1 | 76% | (75.15; 76.83)% |
| 2 | 9.6% | (9.03; 10.19)% |
| 3 | 3.02% | (2.69; 3.37)% |
| 4 | 0.88% | (0.71; 1.08)% |
If this means nothing to you, first, congrats on being able to be certain about things; I miss that. Second, just know that it is likely that the true probability of pal having a given number of skills falls within that range*.
These values came into play while entertaining the possibility that, for any number of skills > 1, the probability is equal to (0.3)^n. It’s a neat and tempting proposal and while possible, these observations render it unlikely.
If you’ll permit some unsubstantiated speculation, however, I do have a theory that the actual skill count distribution is [0: 10.5%, 1: 76.0%, 2: 13.5%] and, if it rolls 2, it will roll again with some probability, repeating on success.
From playing around a bit, 30% and 20% re-roll probabilities seem to match the 3-4 skill counts reasonably well. This would also mean they wouldn’t have to change the logic for pals with 1-2 innate passives since it would only re-roll up to a max of 2 times.
* to those who know better: save your strength. This is among the least egregious of the oversimplifications to come.
Skill Distributions (Q2, Q3)
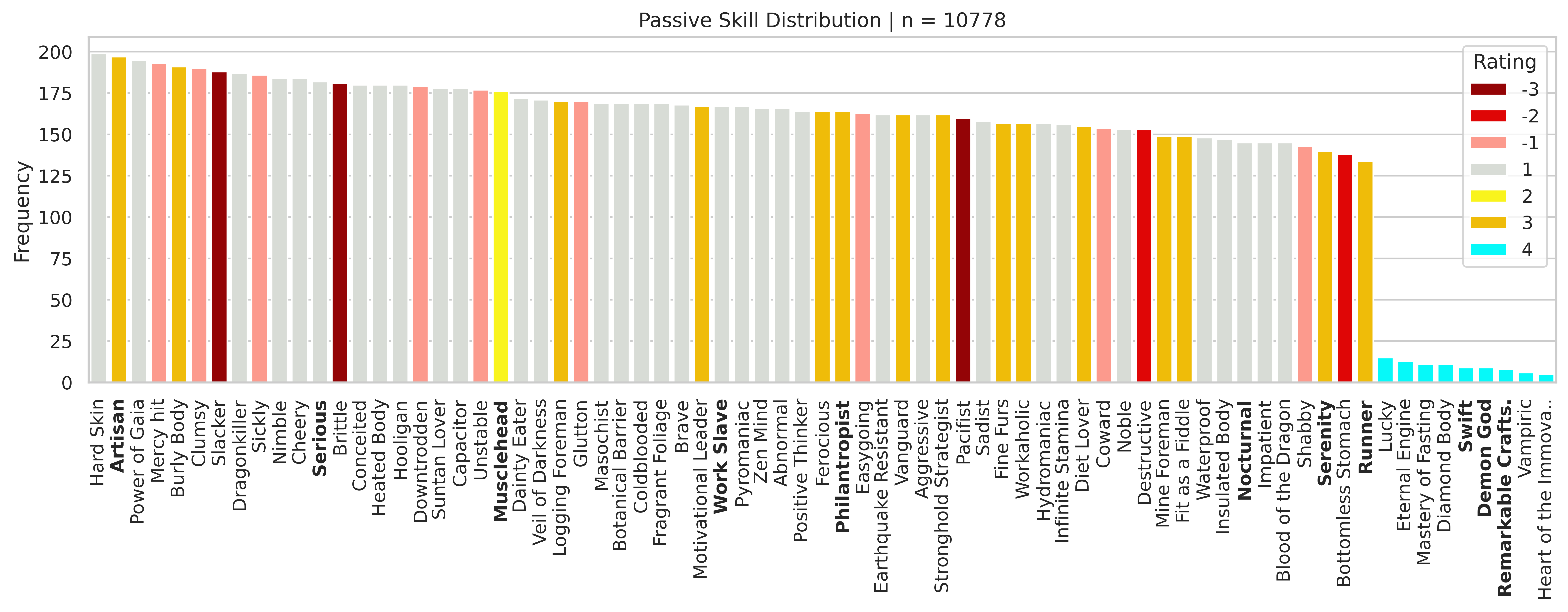
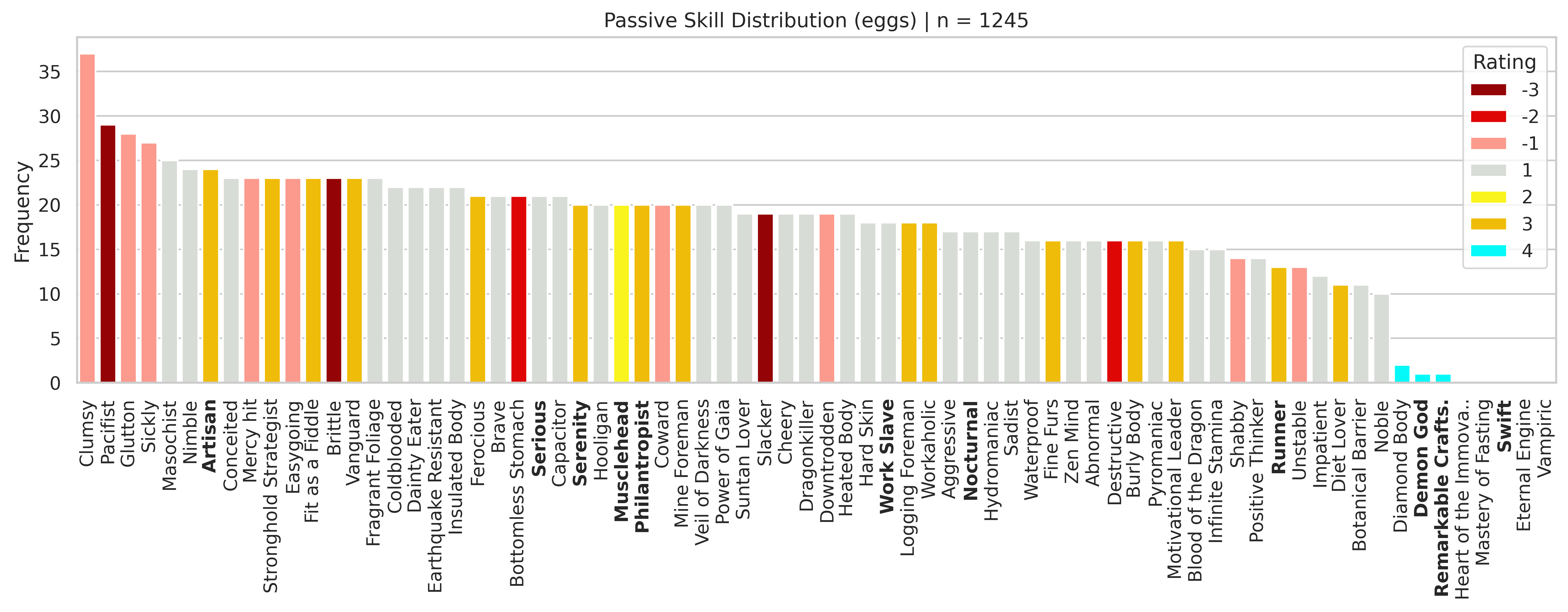
Here we have a flattened count over all skills observed. The keen-eyed among you might notice that there are more skills than pals caught. After taking into account 0 and multiple trait cases, you end up averaging about ~1.08 passives per wild-caught pal.
A cursory glance at this data might lead you to believe that Hard Skin is more likely than Runner, and Rating=-1 is more common than Rating=3. I argue however, that the first statement is not true and the second is not only not true, but the opposite is true. In fact, Rating=3 is the second most common skill group after Rating=1.
If you haven’t figured out where I’m going with this yet, I’ll stop burying the lede. The data suggests that for both Common and Rainbow, all passive skills have an equal probability of being selected within their respective set.
Said another way, passive skills are drawn uniformly at random without replacement from either the set of Common or the set of Rainbow skills, ostensibly with some “rare event” probability determining which. Consequently, the probability of a skill of a particular Rating is proportional to the number of skills with that Rating.
It’ll help to have a small Ratings Table on hand for this explanation. This table shows how many distinct passive skills there are in the game, grouped by passive rating.
| Rating | 1 | 3 | -1 | -3 | -2 | 2 | Total |
|---|---|---|---|---|---|---|---|
| #skills w/ rating | 34 | 15 | 9 | 3 | 2 | 1 | 64 |
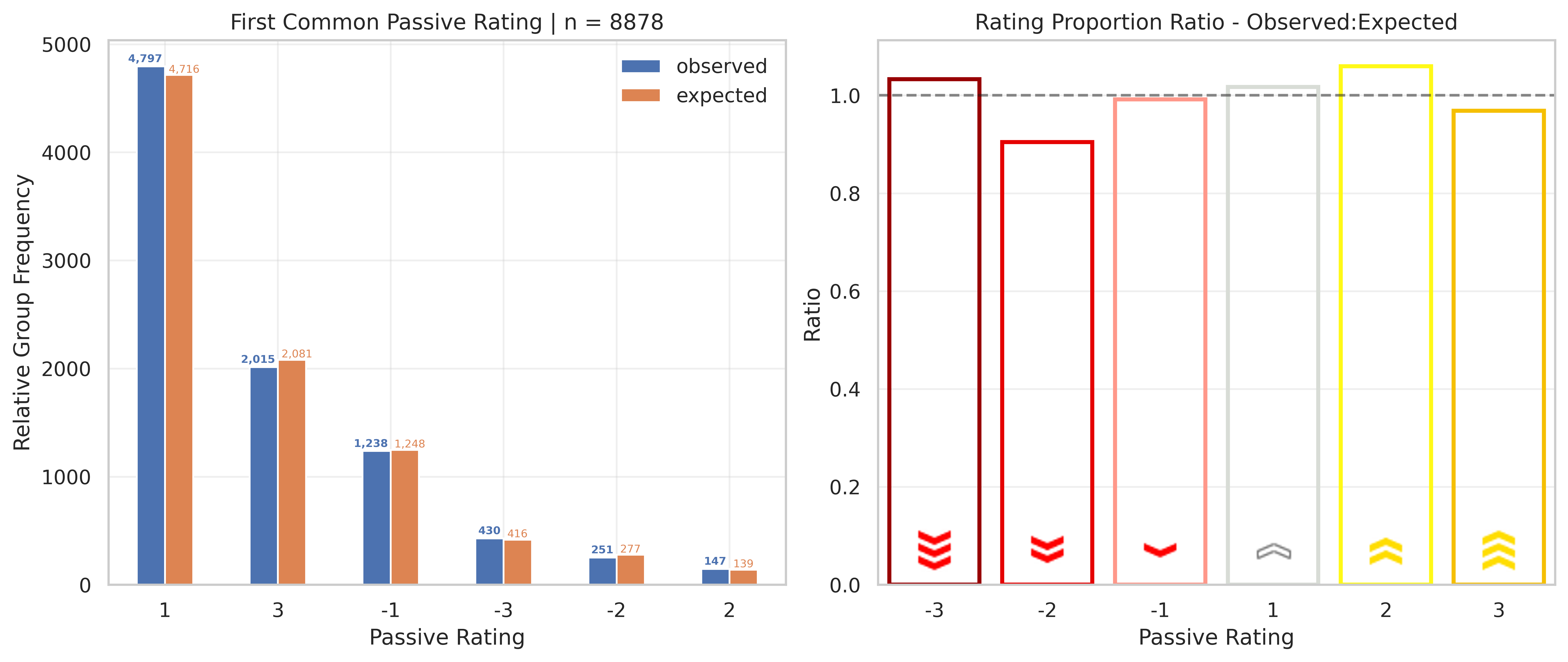
The first thing to note is that the plots are just different representations of the same data. Specifically, they model the number of Common passives in the 1st skill slot with a particular rating relative to the number we’d expect to see assuming uniformity.
The left plot shows two distinct values: observed and expected. The observed is the number of skills with a particular Rating we saw in the 1st passive slot. The expected is the Ratings Table proportionally scaled up to our n=8878.
For example, there is 1 skill with Rating=2 (Musclehead). Assuming uniformity, 1 in every 64 first-slot skills should have Rating=2, on average. Out of 8,878 skills, we’d expect 8878(1/64) = ~139 of them to have Rating=2. What we actually observed was 147 skills. Not far off!
The right plot is simply combines these values (observed/expected) to show relative differences, rather than absolute. Values < 1 mean we saw proportionally fewer skills with a Rating than we’d expect; values > 1 mean there were proportionally more than expected.
Hopefully that’s enough convincing for the lot of you, but for any stat-stickler holdouts: a χ² test over a proportional uniform distribution produced the following:
| Passive Subset | p-value |
|---|---|
| Common | 0.26868 |
| Rainbow | 0.77369 |
| Rainbow (+Lucky) | 0.23167 |
At a significance level of 0.05, we’d fail to reject the null in all cases and therefore have insufficient evidence in favor of the alternative that the relative proportion of skills in each group differs from uniform.
(Word to the wise, this is a blatant misuse of p-values, but if you’re here expecting rigor, you’ll be waiting ‘til mortis.)
Common-Rainbow Probabilities (Q4, Q5)
Unfortunately, my colored rectangles are on cooldown, so some good ol’ fashion tables and lines will have to do for this section. We’ll start by looking at the data from two perspectives - a per capture basis and a per skill basis.
Lucky is begrudgingly included for completeness but is kept separate from the real Rainbow passives and is ignored whenever possible. By questioning this practice, you consent to receive my Lucky rant.
You have been warned.
Per Capture
| Words | Obs. Pal Proportion | Approx. probability |
|---|---|---|
| Blank (0 passives) | 1050 / 10000 | 10.5% |
| At least 1 passive | 8950 / 10000 | 89.5% |
| At least 1 Rainbow | 71 / 10000 | 0.71% |
| At least 1 Common | 8901 / 10000 | 89.0% |
| Lucky | 15 / 10000 |
I won’t hold it against you if you giddy up and go with knowledge that ~1 in 140 wild-caught pals have a Rainbow passive. Though, if you’re anything like me, this just doesn’t quite scratch the itch.
At best, we can say we have an estimate of the probability that a pal has a Rainbow passive, but this doesn’t tell us the actual probability associated with getting a Rainbow passive. If you’re confused, hold tight. If you think this is overly pedantic — welcome to empirical analysis: the game where the probabilities are made up and the points don’t matter.
The mental framework I choose to follow for passive assignment goes like this:
- Decide if the pal is Lucky with some probability we don’t care about.
- Determine the number of skills n by drawing from the number of passive skills distribution in Q1 (clipped at 3 if Lucky).
- For each empty passive slot up to n, pop a passive uniformly at random from the Rainbow set with probability p or the Common set with probability (1-p).
Our goal is to estimate a value for p without having to reverse engineer it from byte code because we are but mere mortals.
Per Skill
One key assumption in my mental framework is that p is fixed and Rainbow and Common sets are isolated. If this is not true and instead something like a weighted selection over all possible skills is used, then the independence assumption is violated, p will depend on n, and all my calculations for n > 1 will be wrong. So,… fingers crossed, I guess? …… maybe we should check it.
So. It appears as though all my calculations for n > 1 will be wrong, and the independence assumption may be violated. After far too much testing, I am mildly confident that there may be some interaction between the number of passives and Rainbow skills that might not support the isolated skill sets hypothesis. Rousing stuff, ain’t it?
From here, we can either spend the next few paragraphs speculating on possible alternative implementations that better fit the data, all while losing equal parts generality and sanity, or say “RNG do be like that sometimes” and roll with what we got.
… I agree. Roll with it is the morally responsible choice. All that’s left now is to figure out exactly how much like that it do be.
| n | Obs. Pal Prop. | MLE_p[Binom(n, )] | P(X≥1); X ~ Binom(n, p=1/149) |
|---|---|---|---|
| 1 | 46 / 7600 (0.00605) | 0.006054 | 50.9 / (7600 * 1) |
| 2 | 14 / 960 (0.01458) | 0.007886 | 12.7 / (960 * 2) |
| 3 | 6 / 302 (0.01987) | 0.006689 | 6.0 / (302 * 3) |
| 4 | 5 / 88 (0.056818) | 0.014368 | 2.3 / (88 * 4) |
We have these Maximum Likelihood Estimates for p given n that just don’t agree. Considering single-passive pals contribute ~22x the number of skills as 4-passive pals, we may want to give them a bit more credence in our estimate.
A straightforward way to do this is to use the MLE for each n weighted by the proportion of skills contributed. Following this gives us p ≈ 0.0067 (~1/149) and a worst case binomial test p-value of 0.087. Not great, not terrible. For n = 1, we’re only about 5 Rainbows shy of expected; for n = 4, about 3 more than expected. That’ll do.
At this point, you may be thinking to yourself, “this is all well and good magic man, but your funny words can’t explain why it takes forever to get the passive I want”.
Au contraire, mon ami. Assuming this estimate for p is accurate, you can expect needing around 3,016 pal captures to collect all 8 unique Rainbows.
Further, in my case the game decided to provide an excellent demonstration of how expectations ≠ guarantees and it took 5,365 pals before I saw a single one with Heart of the Immovable King. Bizarrely, the other 7 Rainbow passives were all collected within the first 669 captures.
Stranger still, would you believe over half of all the Rainbows collected took at most 80 pal captures.
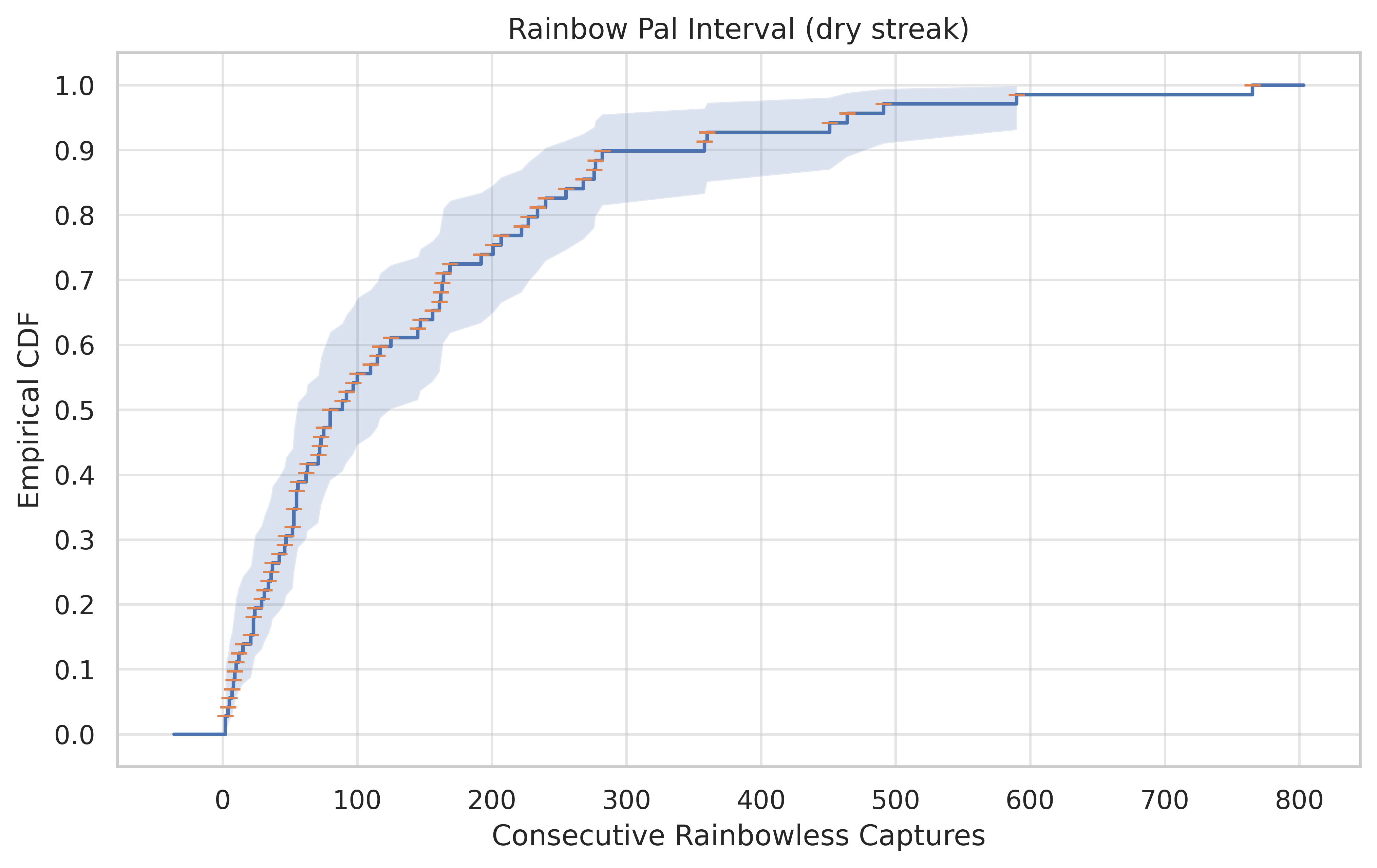
The median was 80 captures between Rainbow pals. The average was 1 Rainbow every 138.5 captures. Such a disparity is usually indicative of outliers wreaking havoc on the good, upstanding citizens of the data.
Lo and behold, the longest dry streak I had was 764 captures without a single Rainbow pal. That’s nearly 100 more captures with 0 than it took to originally collect 7 out of 8 unique Rainbows for the first time. It’s Bonkers I tells ya, and can’t nobody prove me otherwise.
Getting Specific
Rainbow Passives
When it comes to calculating the probability of getting any 1 specific skill, simply dividing the probability of getting any skill in the set by the number of skills in the set will get you pretty close. For Rainbows in particular, this estimate is well within the margin of error, but if we want to be especially obnoxious (and we do) then we’ll need to account for the possibility of getting multiple Rainbows on pal.
Sounds impossible, but get this — exactly 1 out of the 10k pals had a double Rainbow. Using the Q1 n-skill distribution for n > 1 and the value for p we found, the estimated probability of getting 2 or more Rainbows on pal is ~0.00107% or ~1 in 93k captures. Do I regret tossing the one I got? Well, it was Vamp and MoF, so… no.
Change the threshold to 1 or more Rainbows on a pal, and the probability of getting any one specific Rainbow skill can be calculated in almost the same way. The only difference we now need to account for the fact that passive skills are unique.
Technically speaking, we’re playing in hypergeometric land now. Because we’re only interested in 1 skill at a time, however, we can simplify and say it’s the expected number of Rainbows on a pal, divided by the number of Rainbows (8). This amounts to a probability for any single capture to have a specific Rainbow skill of ~0.09% or ~1 in 1110.
Common Passives
In contrast to Rainbows, long-time fans of the game and/or tautologies might know that Common passives are common. As a result, the specific Common passive calculation is influenced far more by the effects of multi-passive pals. Deciding not to ignore this case before means we’re on easy street now.
All we need is the probability associated with getting any Common passive. I bet if we give p a really nice complement, it’ll tell us the probability that a given skill is not Rainbow (aka Common).
Using p-complement (1-p) and the Q1 distribution, we calculate the expected number of Commons on a pal and divide by the number of Commons (64) to get the single-capture specific Common skill probability of ~1.67% or ~1 in 60.
Yakumo (Bonus Round)
If you managed to read all the way to here, pat yourself on the back; that was a lot of information.
If you read the TL;DR and then scrolled right to here, pat yourself on the back; that was a lot of scrolling. In either case, you’re in for a treat.
We’ll now discuss what I believe to be 2 completely novel (or at least little known) facts about how Yakumo’s partner ability “Birds of a Feather” (BoaF) works under the hood.
Dataset
- 1000 Gobfin captures with a max-condensed Yakumo out the entire duration. The Yakumo was bred to have 4 Rainbow-tier passives (EE, Swift, DG, RC) to minimize the influence of random skill rolls.
Background info
- Yakumo’s partner ability makes it “easier to encounter pals with the same Passive Skill as this Pal.” Where “easier” = 30% chance for passive sync when max-condensed.
- A pal’s passive skills are determined on spawn, not capture. By the time you can see a pal in the wild, its passives have already been determined. This is how skill-peak mods can exist.
It’s All Adding Up
1. Yakumo’s partner ability adds passive skills to a pal. It does not replace existing skills
If BoaF were purely substitutional, the average skill count would be unchanged, so we’d expect a skill count distribution exactly like the one in Q1.
If it were additive, the average skill count would go up, the distribution would spread and shift right, and removing the matches would get us back to the Q1 distribution.
If it were both, removing the matching skills from skill counts would result in the majority of pals having 0 passive skills due to many being replaced.
Well, prepare yourself. As far as evidence goes it don’t get much more damning than this —
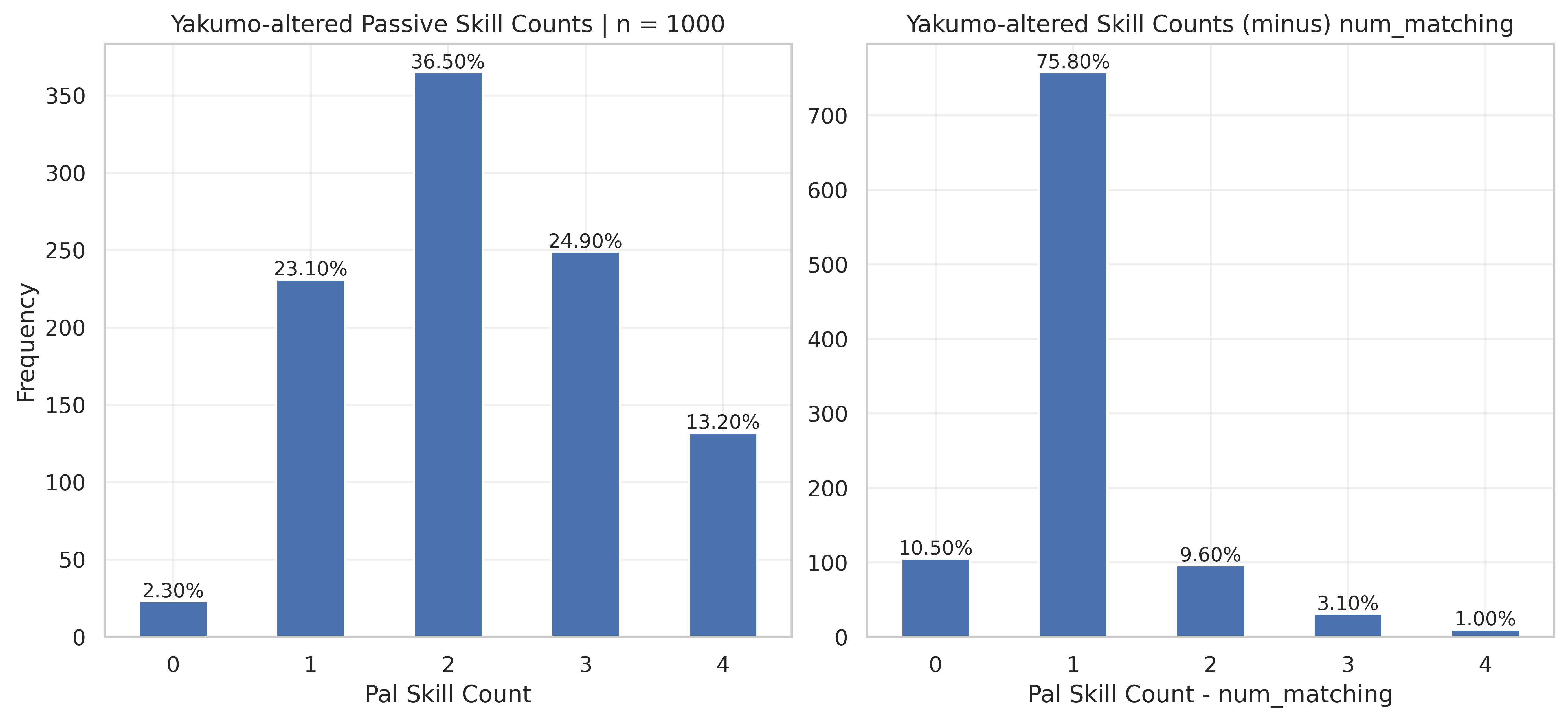
The left chart shows the raw skill count frequencies. The right chart shows the skill count frequencies after removing the 4 Rainbows that matched Yakumo’s set.
You’ll notice that removing the matches recovers a nearly identical distribution to that of Q1. Seriously, scroll back up, I’ll wait. ….
…. You back? Okay cool.
Aside from a little noise from the dataset being 1/10th the size and the possibility that a couple of RNG’d matches were removed, we are just about bang on. I could run a stat test to formalize it, but at this point, I feel like that’s just rude. Myth Busted.
Practical Application
Whenever I had a specific breed chain in mind but was missing 1 pal, I debated if Yakumo would help the hunt even though other pals in the chain already had all the desired passives. Knowing that BoaF can only add skills gives us the answer.
If you need a breeding match that’s either blank or has 100% skill overlap, leave the Yakumo at home. Exclusively being able to add skills means any pal you capture will always have the same or lower chance of breeding a desired skill combination.
More is More
2. Using single-skill Yakumos is not optimal, and the probability of getting m matches is not 0.30^m
Obvious thing out of the way first. We established that it’s additive and cannot overwrite any existing skills. You might guess that would mean the probability is actually 0.30^min(4-n, m), where n is the number of skills a pal starts with and m is the number of matching skills.
Although that’s a good guess, and your participation is both noted and appreciated, that’s not quite right. The good news is the devs love us a little more than that. The bad news is the binomial distribution is back. And this time… It’s probable.
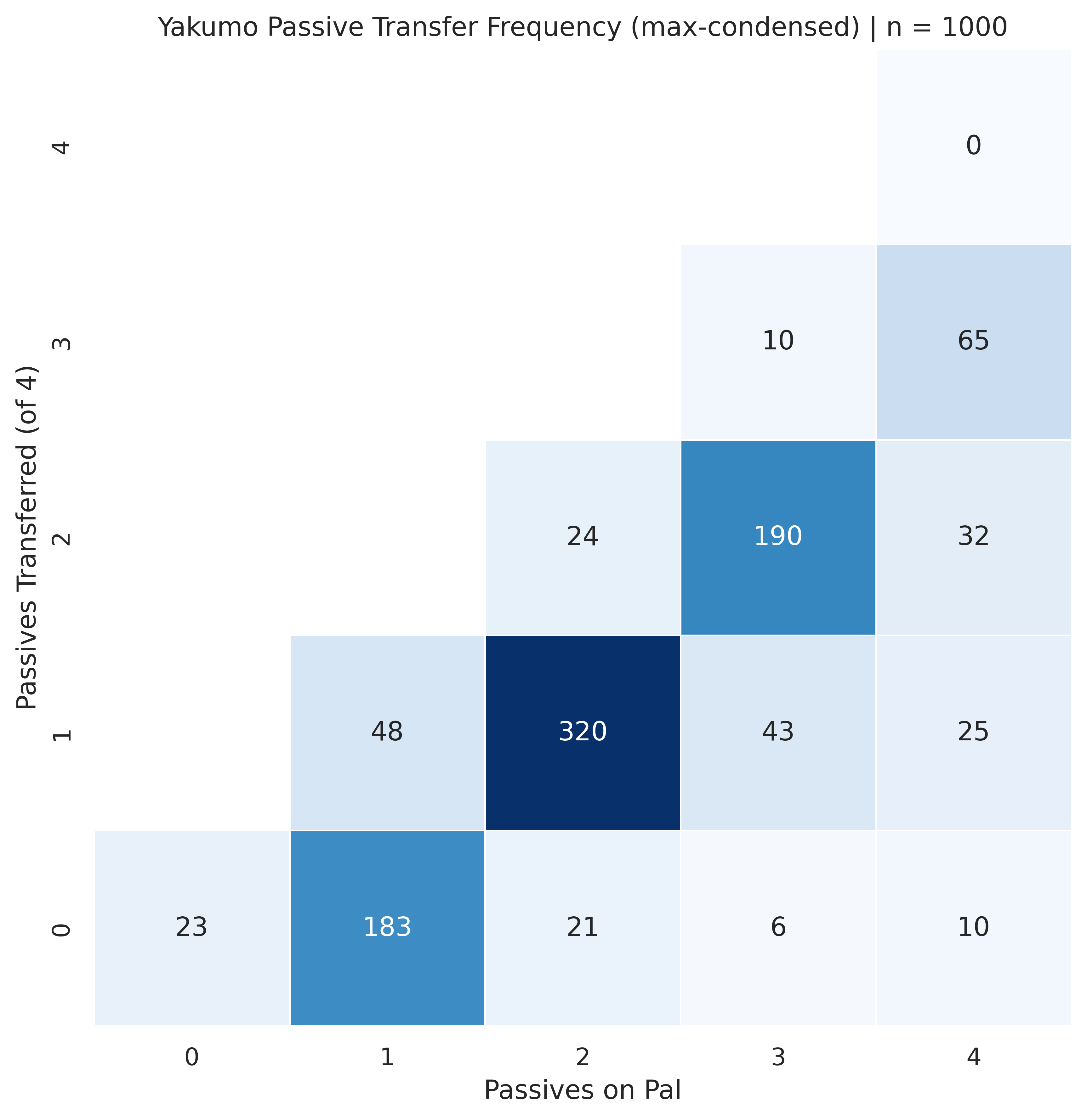
The heatmap above shows the breakdown of how many skills Yakumo’s partner ability contributed to the total number on each pal. The darkest diagonal corresponds to the most common case where the pal starts with 1 passive skill and then BoaF appends between 0-3 additional skills. Above that diagonal is the 0-initial passives case, and below is the 2-initial passives case, and so on.
These results strongly suggest that BoaF rolls once for every passive skill on Yakumo while passive slot space remains. It does not stop if a skill fails to transfer. This means the probability of transferring m out of M passives is better modeled by p[X=m]; X~Binom(n=M, p=0.30) rather than 0.30^m.
I’m sure you all remembered to bring in your personal favorite statistical software today, but just in case, here’s a handy-dandy table to take with you on your travels.
| M (#yakumo) \ m (#hits) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 4 | 24.68% | 41.85% | 26.23% | 7.16% | 0.085% |
| 3 | 34.88% | 44.36% | 18.42% | 2.33% | |
| 2 | 49.45% | 41.90% | 8.65% | ||
| 1 | 70.26% | 29.74% |
These are the probabilities for transferring any subset of m out of M total passives from Yakumo to the target pal after adjusting for expected skill capacity (free passive slots).
For all m < 4, the relative difference from Binom(n=M, p=0.30) is fairly small, but because only 10.5% of pals have 4 free slots (aka start with 0-passives), the odds of a perfect 4/4 match are reduced by nearly an order of magnitude.
This helps explain why there wasn’t a single perfect match out of 1000 captures. Given a probability this low, only about 1 in every 1176 captures would transfer all 4/4 skills on average.
For completeness’ sake, here’s a brief rundown of the implementations considered
- Roll once per Yakumo skill
- The best guess given the data.
- Roll once per free slot
- If this were true, distribution would be a lot closer to Binom(p=0.3, n=3), considering 76% of pals have 3 free slots. We’d also expect pals with 1 free slot to only hit 30% of the time compared to 80% shown in the data.
- Roll a constant 4x regardless of the number of free slots and skills
- No way to differentiate from the data, but this would mean a 1 passive Yakumo would have a 0.7599 * 0.9912 ≈ 75.3% transfer chance on each capture. Anecdotally speaking, yeah… no.
- Roll max(free slots, yakumo passives)
- Again, no way to differentiate from the data, but the single passive Yakumo in this case would still hit about 63.7% of the time, which still seems unrealistic.
Practical Applications
Optimal Setup
Let’s assume you want to transfer 4 passives to a pal.
The optimal setup is to have 1 max-condensed Yakumo for every unique combination of passive skills. Start with the 4 passive Yakumo. Once you get at least 1 hit, switch to a Yakumo that has all the passives that didn’t transfer. Repeat until all 4 passives are collected and then breed away.
Following this idealized approach, on average, you’d need to capture 6.5 pals to transfer all 4 passives to the target.
Despite only ever needing to use at most 4, you’ll have to have 1+4+6+4 = 15 max-condensed Yakumos in order to achieve full coverage. So if you’re cool making enough puppy mash to make Cruella de Vil look like a level 5 hyper-vegan, that’s the way to do it.
Now, maybe you’re not keen on the idea of making all that dog soup; fear not, you can still reap some benefits with only a fraction of the canine liquefaction.
Realistic Setup
Once you get to the point in the game where your ability to max-condense multiple copies of the same pal is limited only by the love you have for yourself, there are very few instances in which you’d actually need BoaF to transfer 4 passives to a pal.
When you’re best option is max-condensing Yakumos, it probably means that the pal you’re after cannot be bred into. Excluding pals that randomly fall out of the sky, 4 out of 5 capturable, self-breed-only pals are legendary pals, which typically need at most 3 skills transferred.
Your goal now is to transfer 3 passives to a legendary pal, for example [Swift, EE, Runner] on a Jetragon.1
Just as before, the optimal setup is to have a Yakumo for every unique combination of skills (1+3+3 = 7 Yakumos) and would take an average of 7.71 captures for all 3 to transfer. But you’re not here for optimal, you’re here because you are lazy care deeply about preserving the solidity of your Yakumos. I respect that and am here to tell you that, contrary to popular belief, your next best option isn’t 3x 1-passive Yakumos, it’s 1x 3-passive Yakumo.
These are the expected number of captures required to transfer 3 skills to a 2-innate pal under each of the no-overlapping-skills configurations
- 1-passive Yakumo → 1-passive Yakumo → 1-passive Yakumo= 11.56 captures
- 2-passive Yakumo → 1-passive Yakumo = 10.65 captures
- 3-passive Yakumo = 9.68 captures
Ultimately, the reason behind this is exactly what you’d expect. When each skill rolls independently, more skills = more rolls = more opportunities to transfer a skill. It also doesn’t hurt that there is a (small) chance to have 2 skills transfer in one capture — a suspiciously rare outcome with 1-passive Yakumos.
Do note, however, that this all is assuming that you are starting from scratch. It’s always better to switch to a max-condensed Yakumo with a smaller subset of desired skills if you have one.
For example, if you happen to get EE using your [Swift, EE, Runner] Yakumo and you have a max-condensed [Swift, Runner] Yakumo lying around, you should switch to maximize your chance of completing the set.
1 At most 2 skills can transfer at a time due to innates. This example uses the previously speculated 2-innate passive skill distribution: [0: 10.5%, 1: 76.0%, 2: 13.5%]. The table below shows the adjusted n-skill transfer probabilities for a 2-innate pal.
| M (#yakumo) \ m (#hits) | 0 | 1 | 2 |
|---|---|---|---|
| 4 | 34.27% | 62.07% | 3.66% |
| 3 | 43.17% | 54.56% | 2.27% |
| 2 | 55.89% | 43.17% | 0.945% |
| 1 | 74.05% | 25.95% |
Breeding Eggs (μBonus)
Initially, this was going to be a fully fleshed out section like Yakumo, but 1) this post is already ungodly long, 2) there isn’t enough data to draw particularly strong conclusions, 3) — and this is key — I don’t really feel like it.
With that ethos in mind, let’s get into it.
Dataset
- 1237 Gobfin eggs produced by 16 distinct pairs of blank Gobfin parents. No eggs were incubated; all were analyzed pre-hatch.
Blank Expressions
1. Myth Bustin’ - You absolutely can breed a 0-passive pal.
I’ve seen a handful of debates between people on the topic of breeding blank pals. The general consensus seems to be that it’s either not possible or extremely rare. It’s high-time we dispel that rumor. Not only is this possible, in my case, it was by far the most common outcome.
Impressed yet? Because you really shouldn’t be. Remember, both parents have 0-passive skills, so all this really shows is that 40% of the time the child will draw from the skill pool of the parents, even if that pool is the empty set. I suppose you could argue this provides some new information, but that slightly depends on your view of words like ‘new’ and ‘information’.
What this does give us, however, is proof that the well-renowned Breeding Probabilities Calculator is wrong. Strictly speaking, [0,0,0]; [0,0,1]; [0,0,2]; [0,0,3] are all valid inputs and should be 40%, 30%, 20%, and 10%, respectively. Is this useful information in 99.997% of cases? Absolutely not. But technically, it is the best kind of correct.
Also, ain’t it cool to see how close the randomly sampled data comes to the known [40,30,20,10], reverse-engineered distribution that our forefather u/mgxts bestowed unto us long ago?
Wild Breeding Mutations
2. Are random breeding mutation and wild-caught passive skills drawn from the same distribution?
¯\_(ツ)_/¯
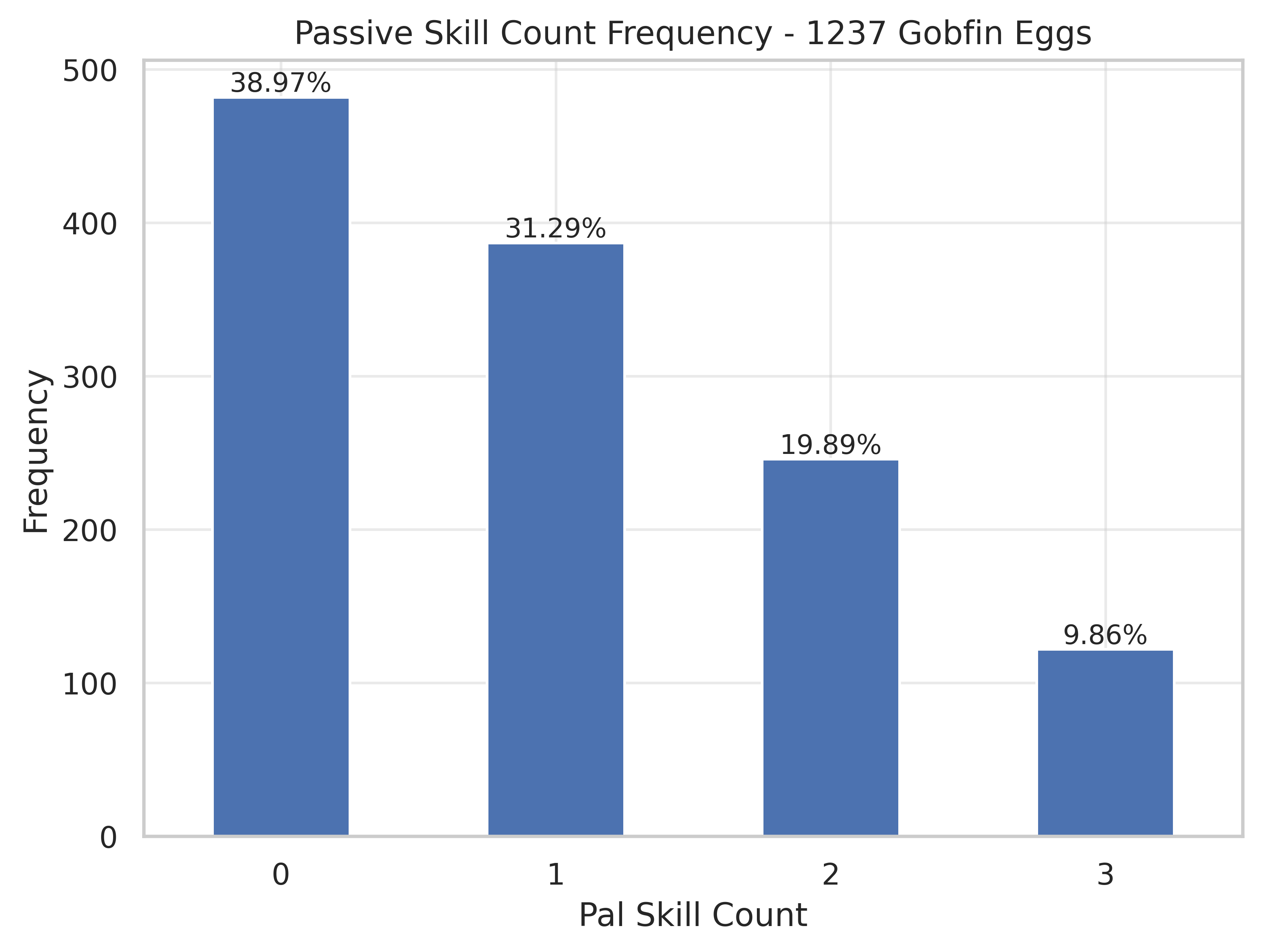
More specifically: probably. For Common skills, I can back that up. For Rainbow skills… it’s all v i b e s.
We can play the same game as before and run a goodness-of-fit test over the uniform distribution and first slot Common passive skill counts. This time around, we’ll go with the slightly more robust G-test rather than χ² because these shark kids are all thumbs.
A G-test over the proportional uniform gives a p-value of 0.38828. Just like last time, this doesn’t confirm it’s uniform, but it does hint at the possibility that it’s not-not-uniform! Hmm…Your eyes seem to have glazed over there.. Okay, how about we take a more direct approach.
Using the contingency table formulation, we can directly compare the expected frequencies of the egg-group and wild-group. In doing so, we find a p-value of 0.79464, meaning that we fail to reject the null even harder. You love to see it. The null in this case is that the relative frequencies in the groups are the same, i.e., Common passives occur with the same frequency in both the case of wild-caught and breeding-mutation skills.
To put a wrap on it, I’ll say, although there’s insufficient data to make any claims about the breeding Rainbow 🌈⭐, the lazy developer in me says there’s a good chance it’s the same. Why use many number when 1 do trick?
There were a total of 4 Rainbows across the 1237 eggs examined. You can peek at the table below to see which ones, along with my manually-collected, almost-certainly-wrong “data” I gathered while trying to breed a perfect Jetragon a while back.
| Rainbow Skill | Gobfin Eggs (n=1237) | Unreliable Jetragons (n=934) |
|---|---|---|
| Demon God | 1 | 2 |
| Diamond Body | 2 | 1 |
| EE, HotK, MoF | - | - |
| Remarkable Craftsmanship | 1 | 1 |
| Swift | - | - |
| Vampiric | - | 1 |